跳至主要内容

[Graph] 1. 什麼是 Graph?

什麼是 Graph?​

Graph 只是一堆 nodes + connections，如下面 4 個圖，都可以算是 Graph：

graph-illustration-1
graph-illustration-2
graph-illustration-3
graph-illustration-4



Graph 的使用情境​

Graph 充斥在我們生活周遭，以下是一些常見的例子：

  • 社交網路 (Social Network)
  • 地址 / 地圖 (Location / Mapping)
  • 路由演算法 (Routing algorithm)
  • 階層視覺畫 (Visual Hierachy)
  • 檔案系統優化 (File System Optimizations)
  • 任何地方



Graph 的術語和種類​

術語​

Graph 的主要術語如下：

  • Vertex：一節點 ( a node )
  • Edge：連結 (connection)
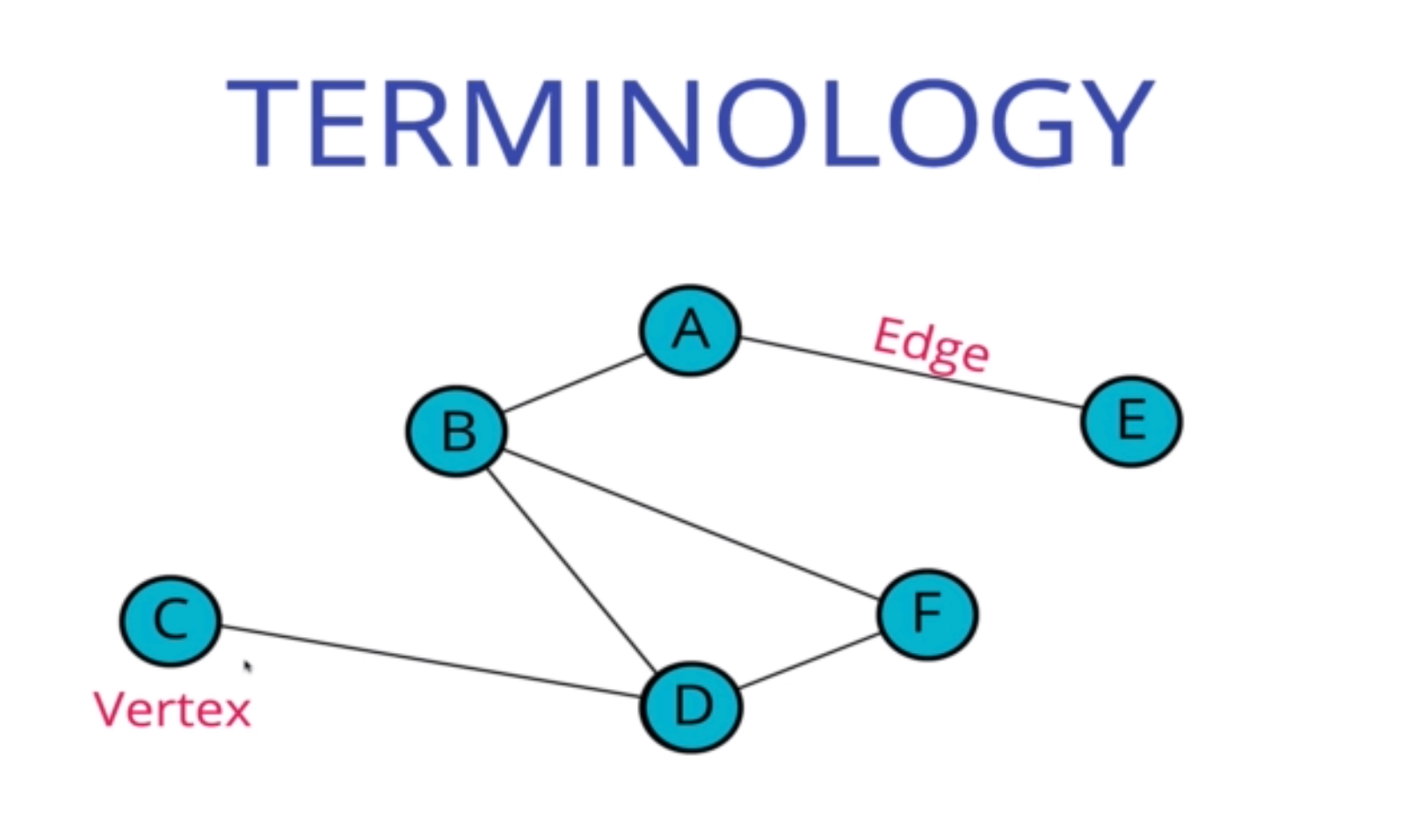
graph-terminology

種類​

  1. Undirected Graph：沒有方向的 Graph

例如：Facebook 的 Friend 關係，Maria 是 Armie 的朋友，Armie 也是 Maria 的朋友，雙方都看得到彼此的動態

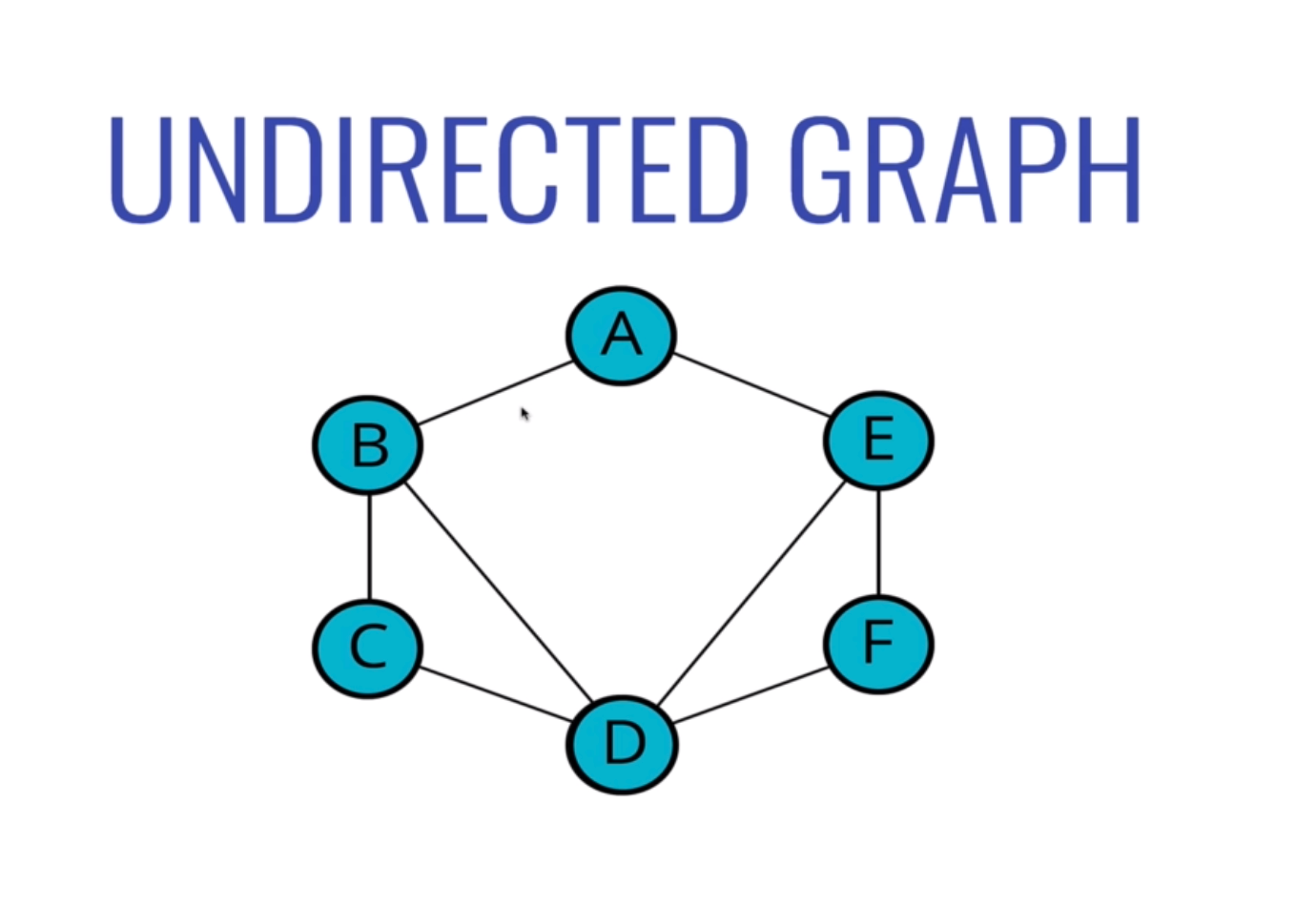
undirected-graph
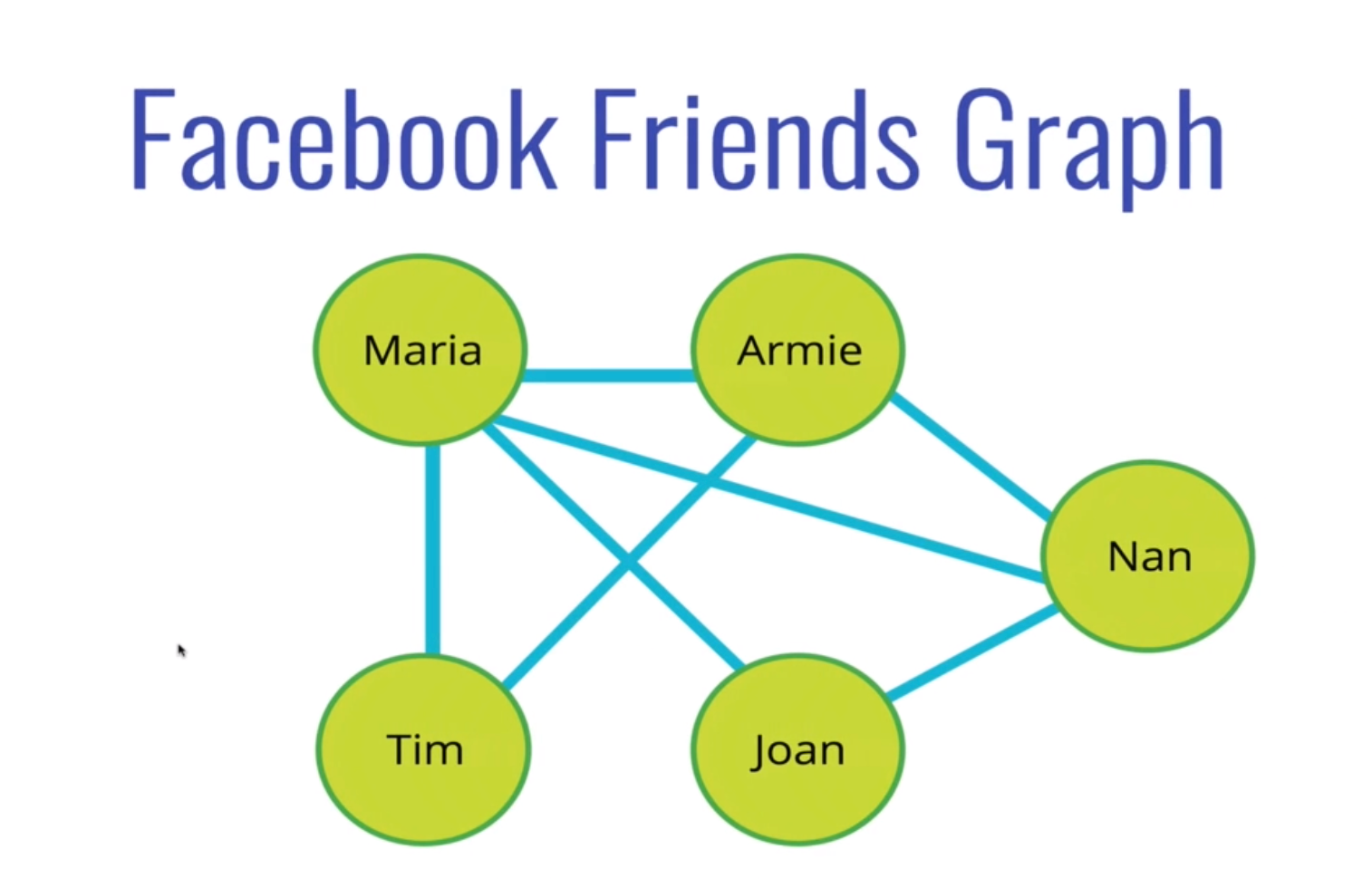
undirected-graph-example



  1. Directed Graph：有方向的 Graph

例如：Instagram 的 Follow 關係，Maria 關注 Justine Bieber，Marie 看得到 Justine Bieber 的動態，但 Justine Bieber 沒有追蹤 Maria，所以看不到 Maria 的動態

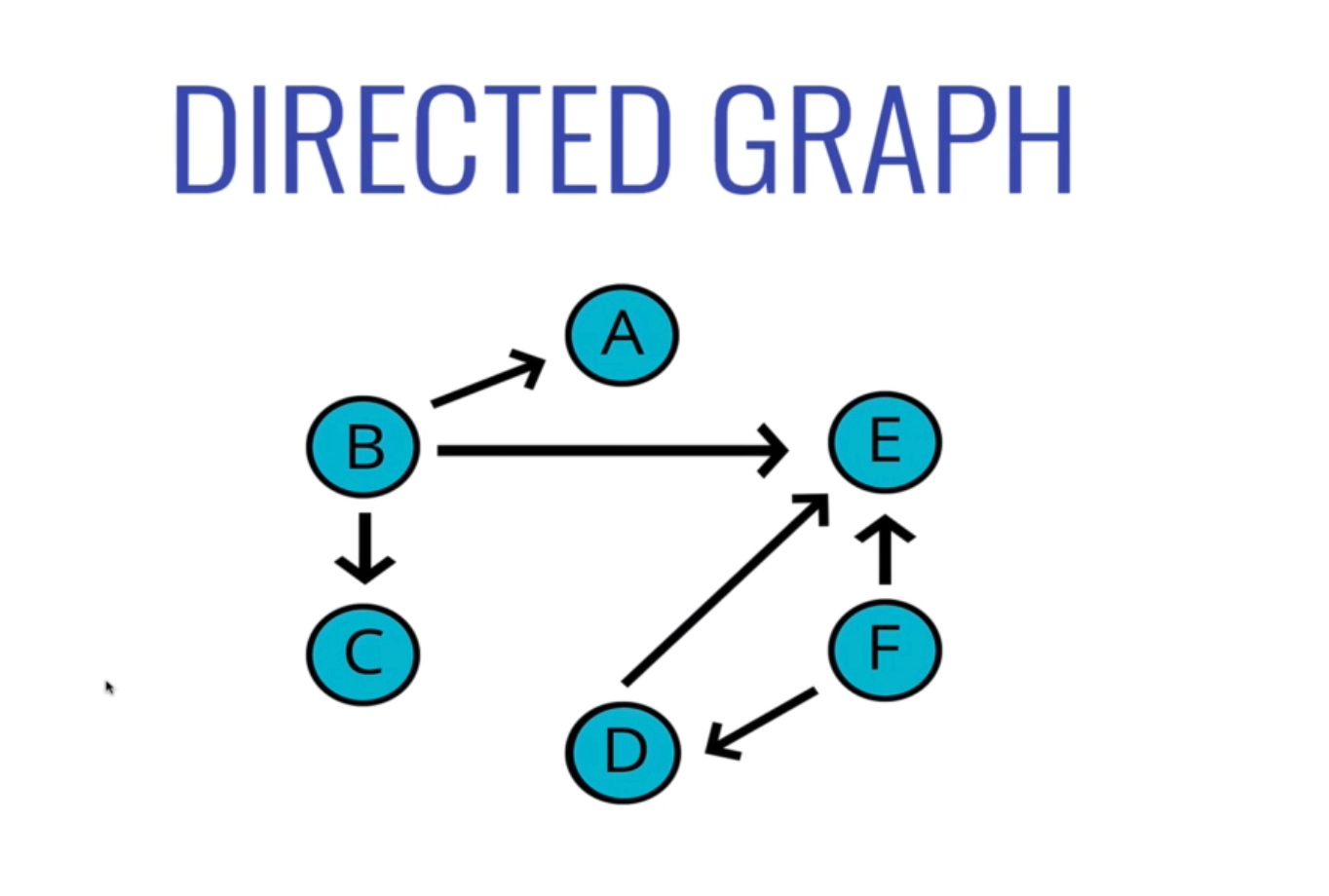
directed-graph
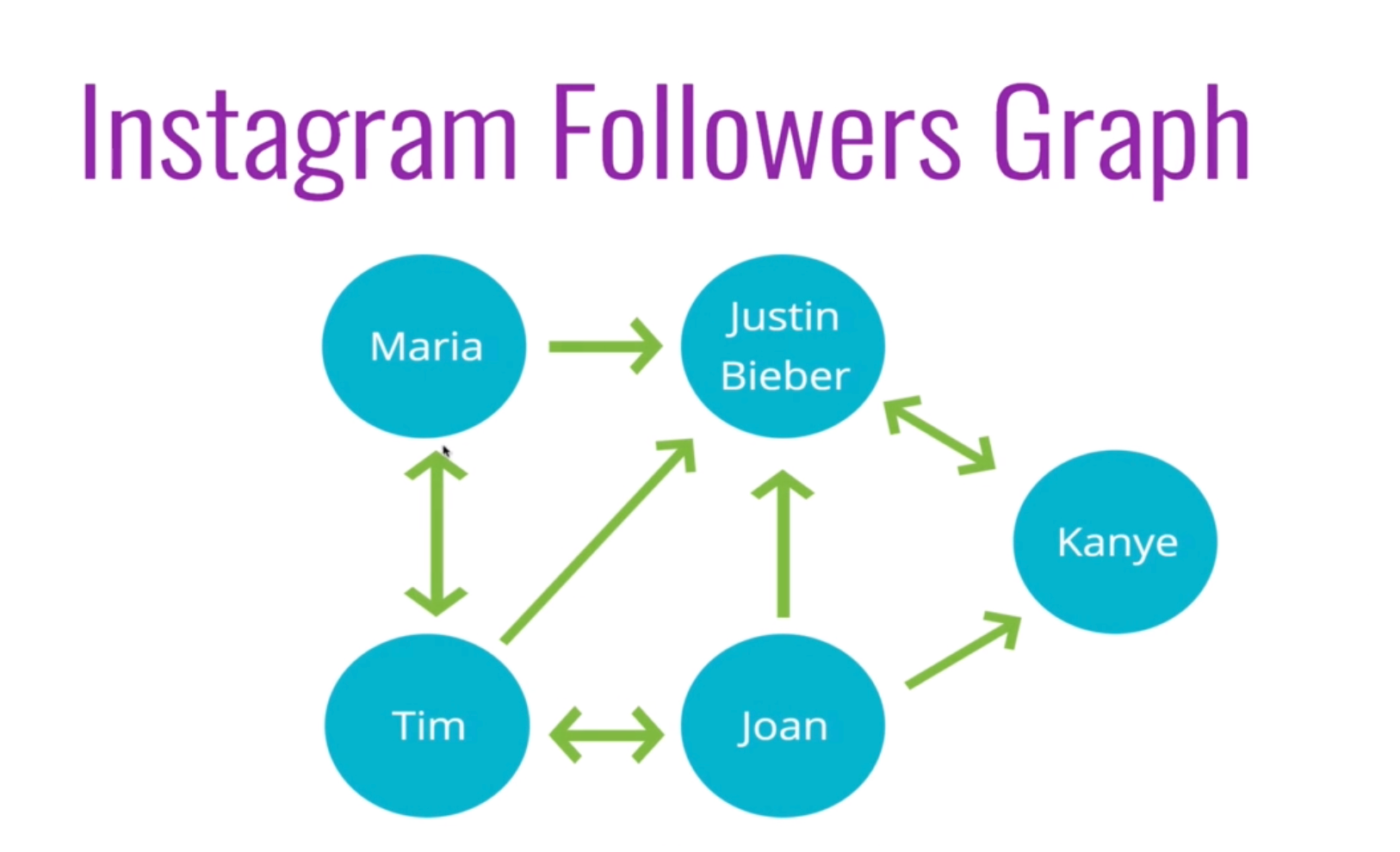
directed-graph-example



  1. Weighted Graph：每個邊 (Vertext) 有被分配特別數字的 Graph，此數字即是所謂的權重 (Weight)

例如：地圖的距離，從台北到上海的直飛航班，距離是 1000 公里，但從台北到上海的轉機航班，距離是 2000 公里

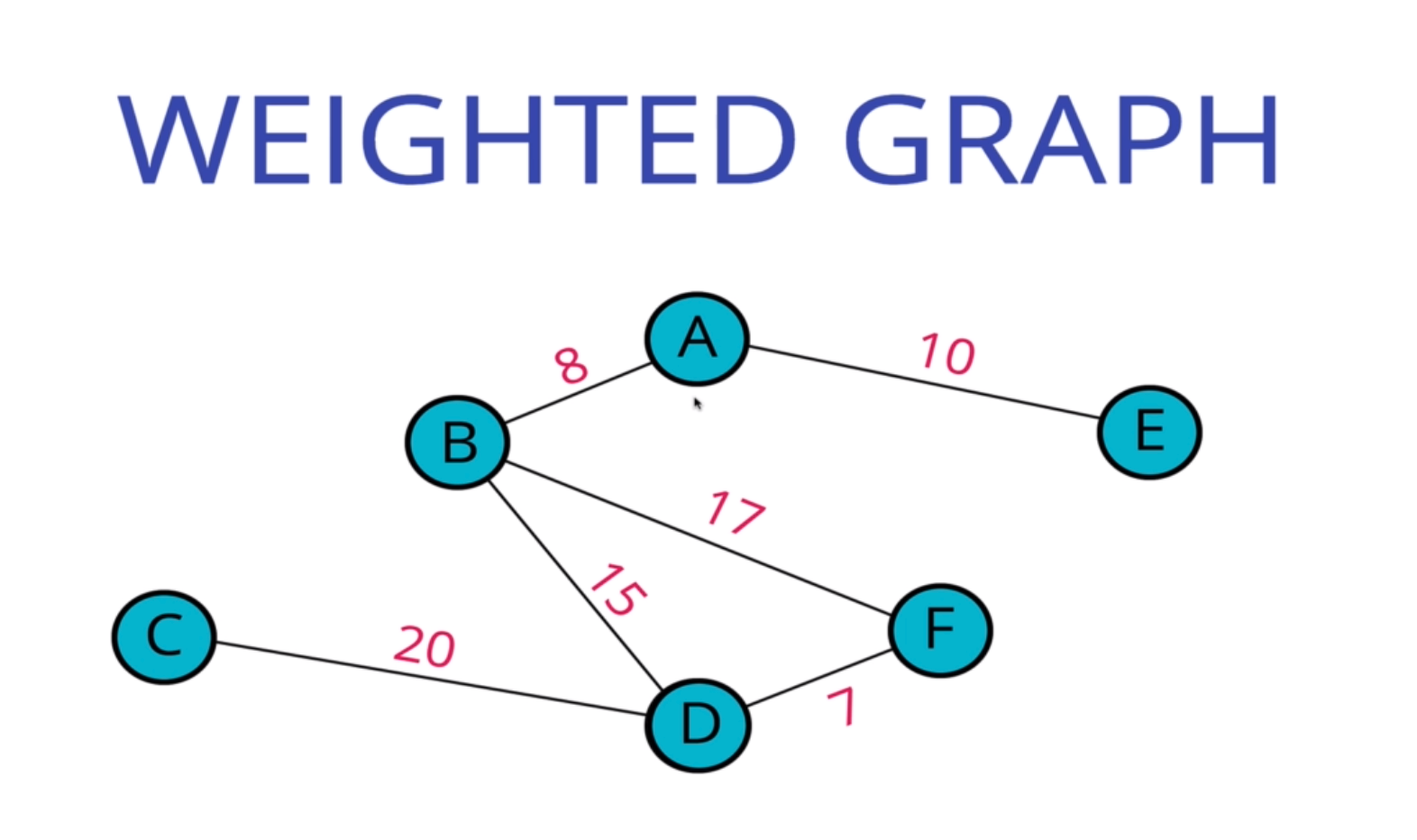
weighted-graph
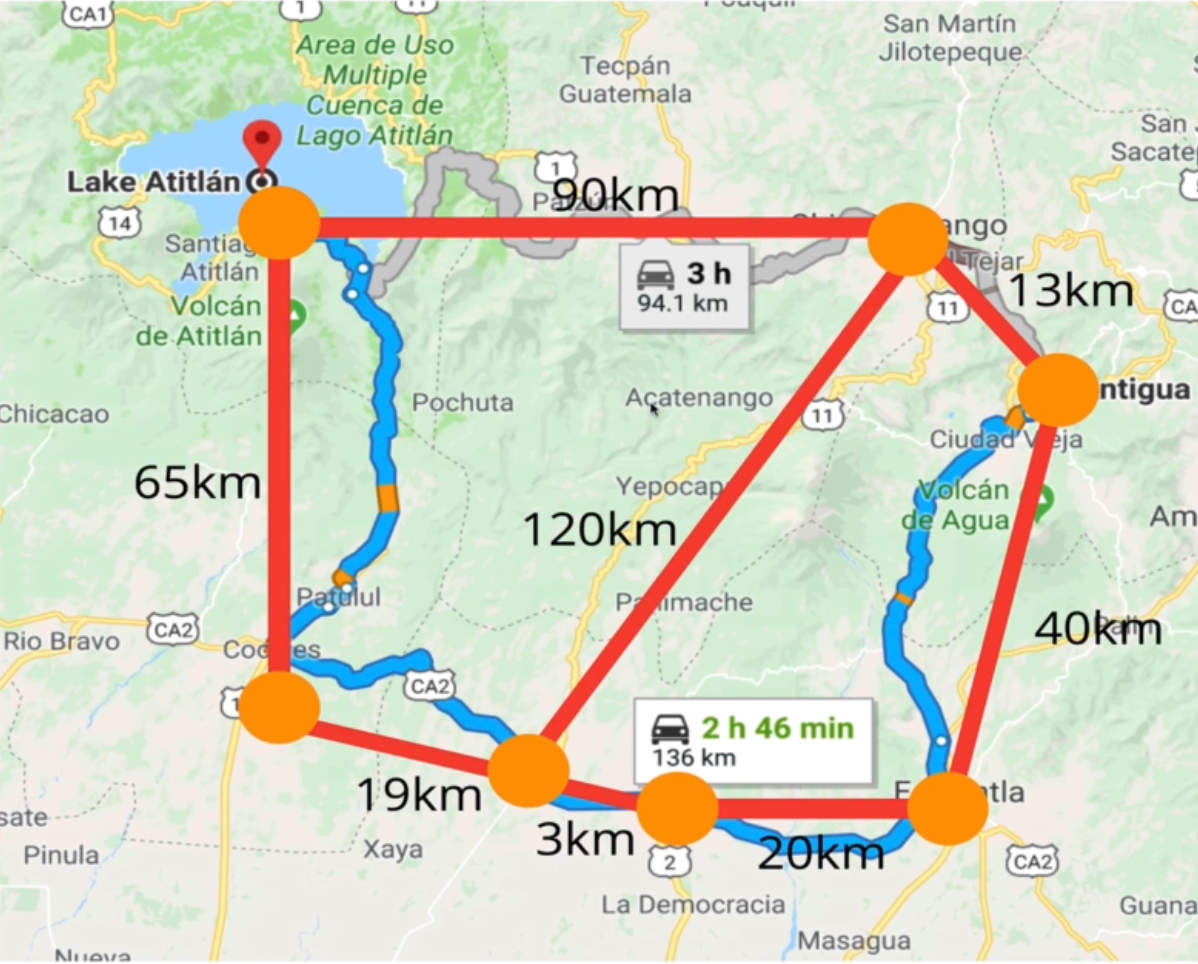
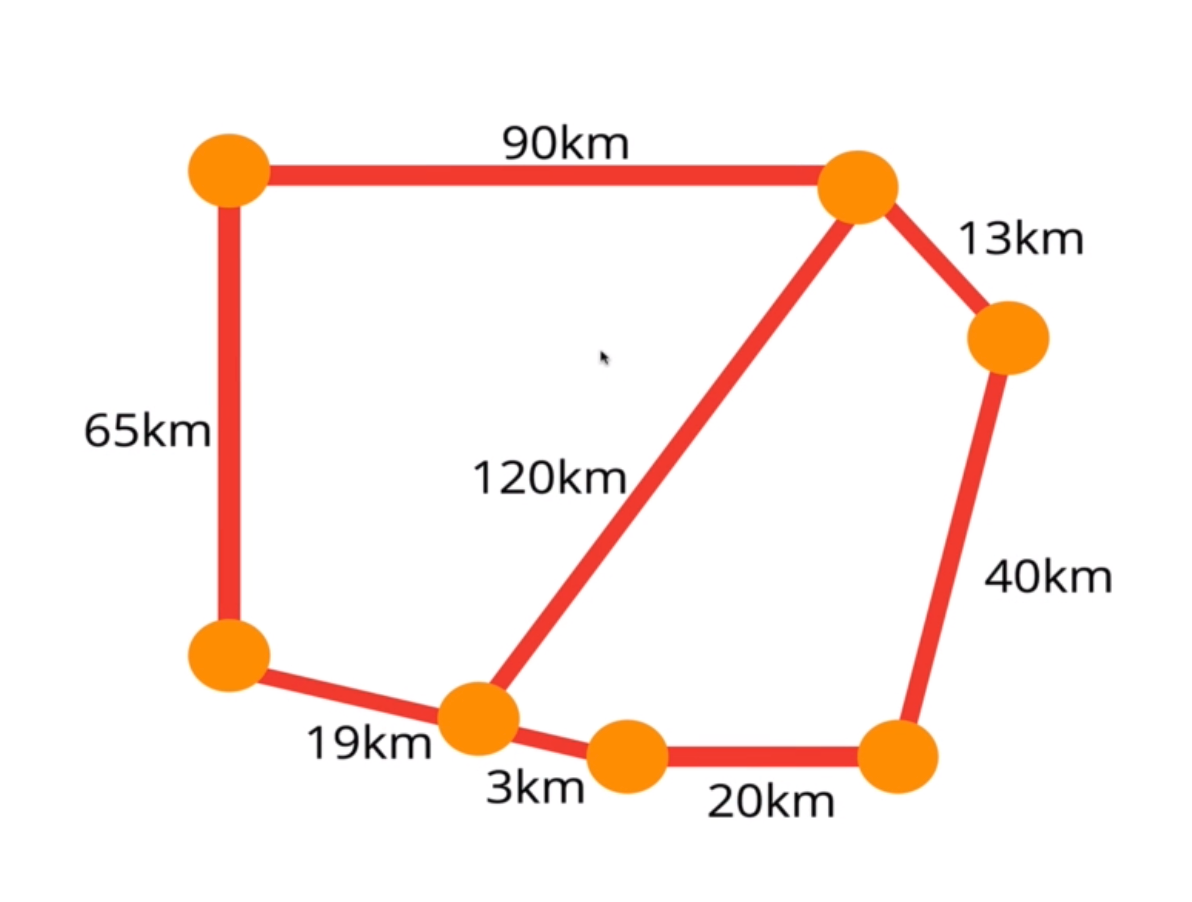
weighted-graph-example
weighted-graph-example



圖的表示法​

圖的表示法主要可以分為以下兩種：

  • 鄰接矩陣 (Adjacency Matrix)
  • 鄰接串列 (Adjacency List)


鄰接矩陣 (Adjacency Matrix)​

Adjacency Matrix 即是用一個矩陣，來表示每個 Vertex 之間 Edge 的連結關係

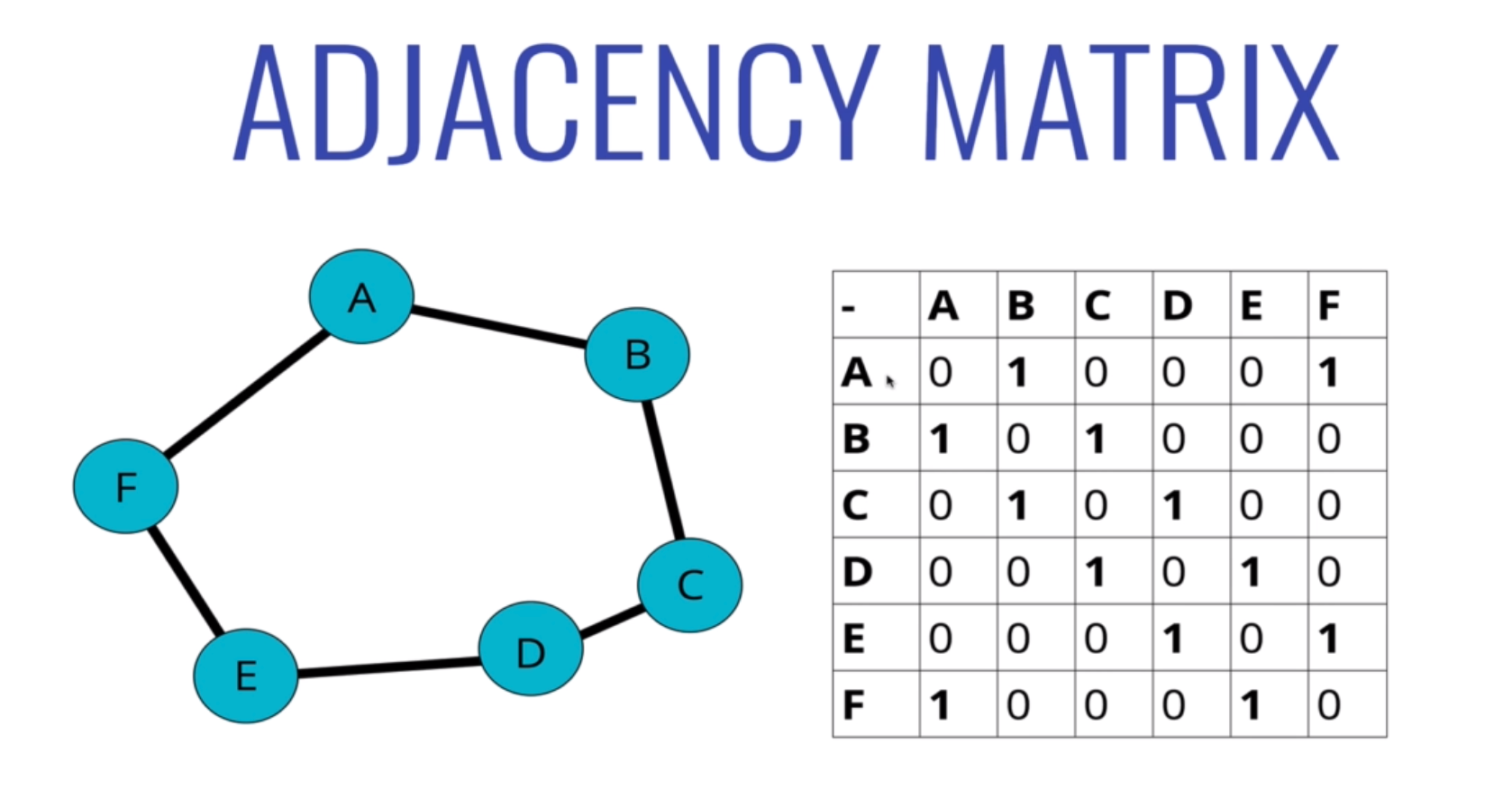
adjacency-matrix-illustration



再根據 Graph 的種類，對應到的矩陣也會有所不同：



  • Undirected Graph：

undirected Graph 因為是雙向的，所以 Matrix 是對稱的，例如當 5 連到 4 時，4 也會連到 5，所以矩陣會是對稱的

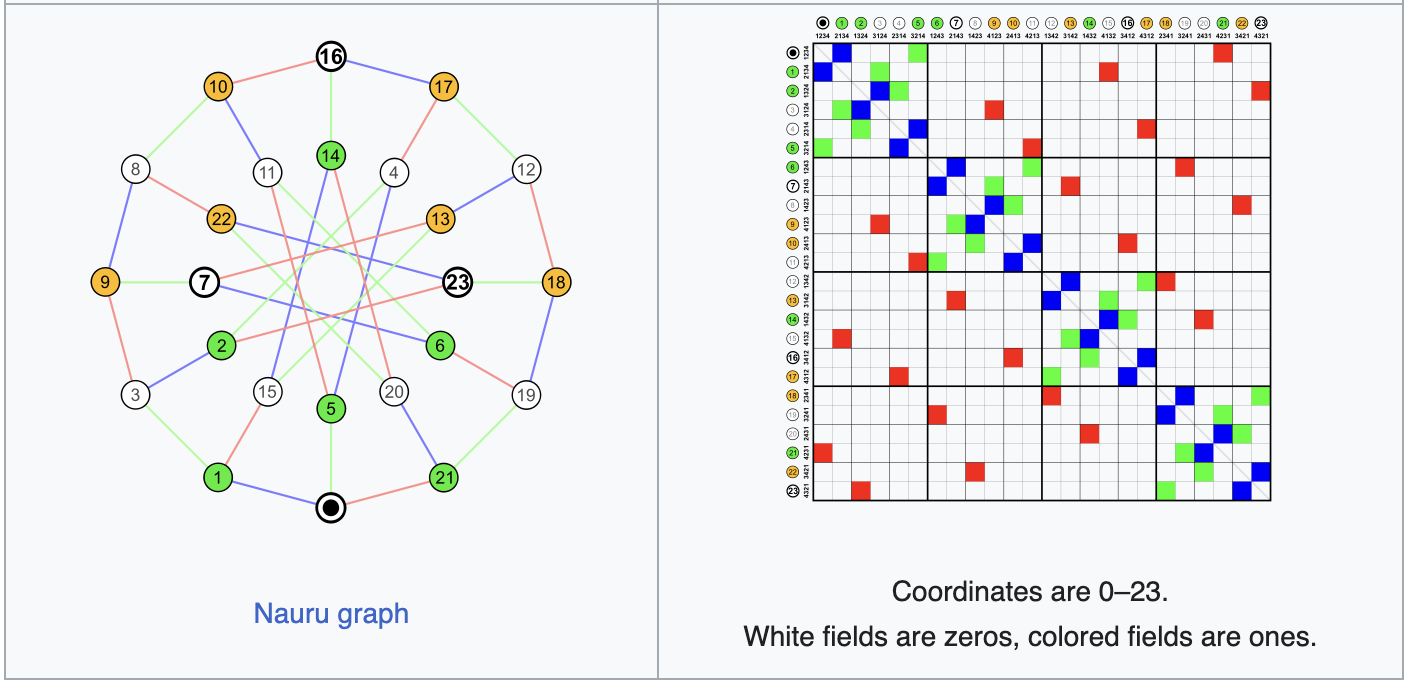
adjacency-matrix-undirected-graph



  • Directed Graph：

directed graph 因為 vertex 之間有單向的，所以 matrix 不會完全對稱，例如當 1 連到 2 時，2 沒有連到 1，所以矩陣就會是非對稱的

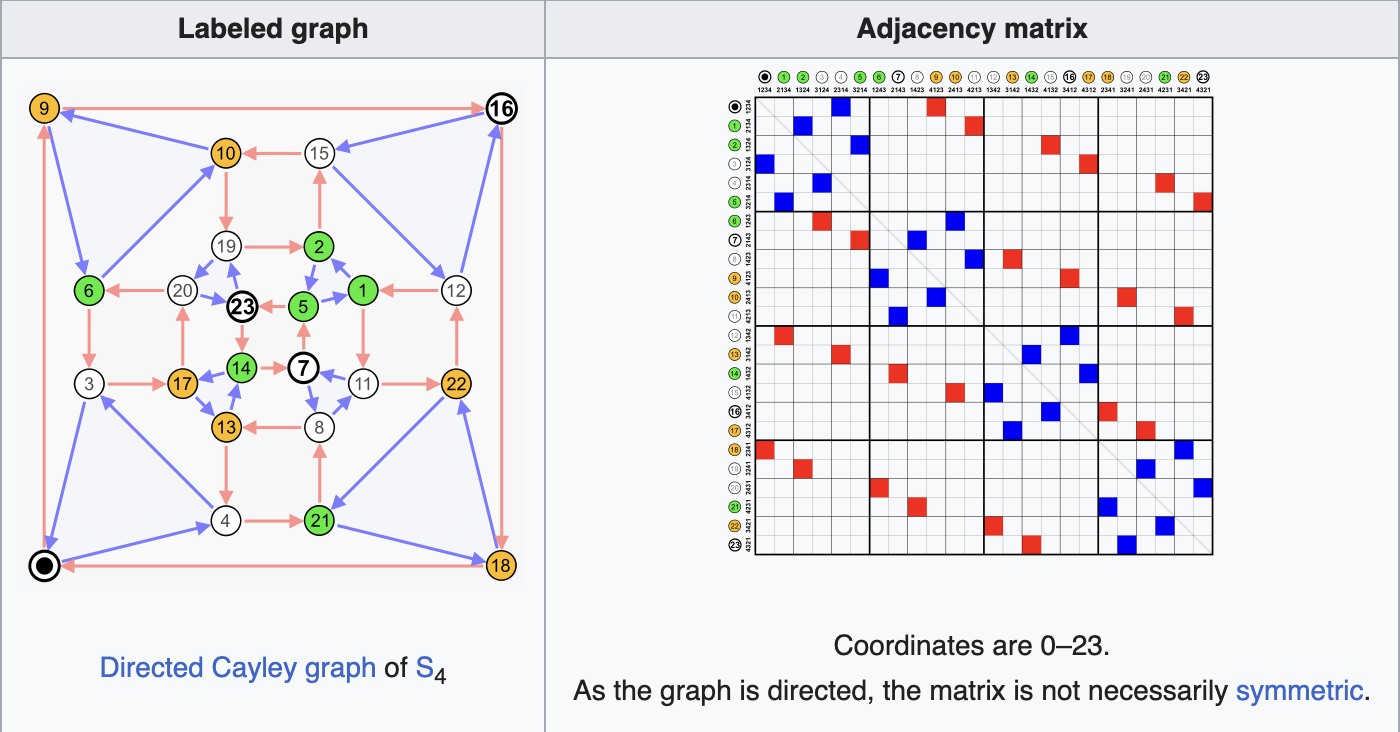
adjacency-matrix-directed-graph



鄰接串列 (Adjacency List)​

Graph 也可以用鄰接串列（Adjacency List）來表示。 其中每個索引代表一個頂點（Vertex），而對應的值是一個陣列，表示該頂點的邊（Edge）及其連接的頂點。例如：

  • 在 0th index 的 Vertex 有連到 1st 和 5th Vertex，在 Adjacency List 就會是 [1, 5]
const adjacencyList = [];

adjacencyList[0] = [1, 5]
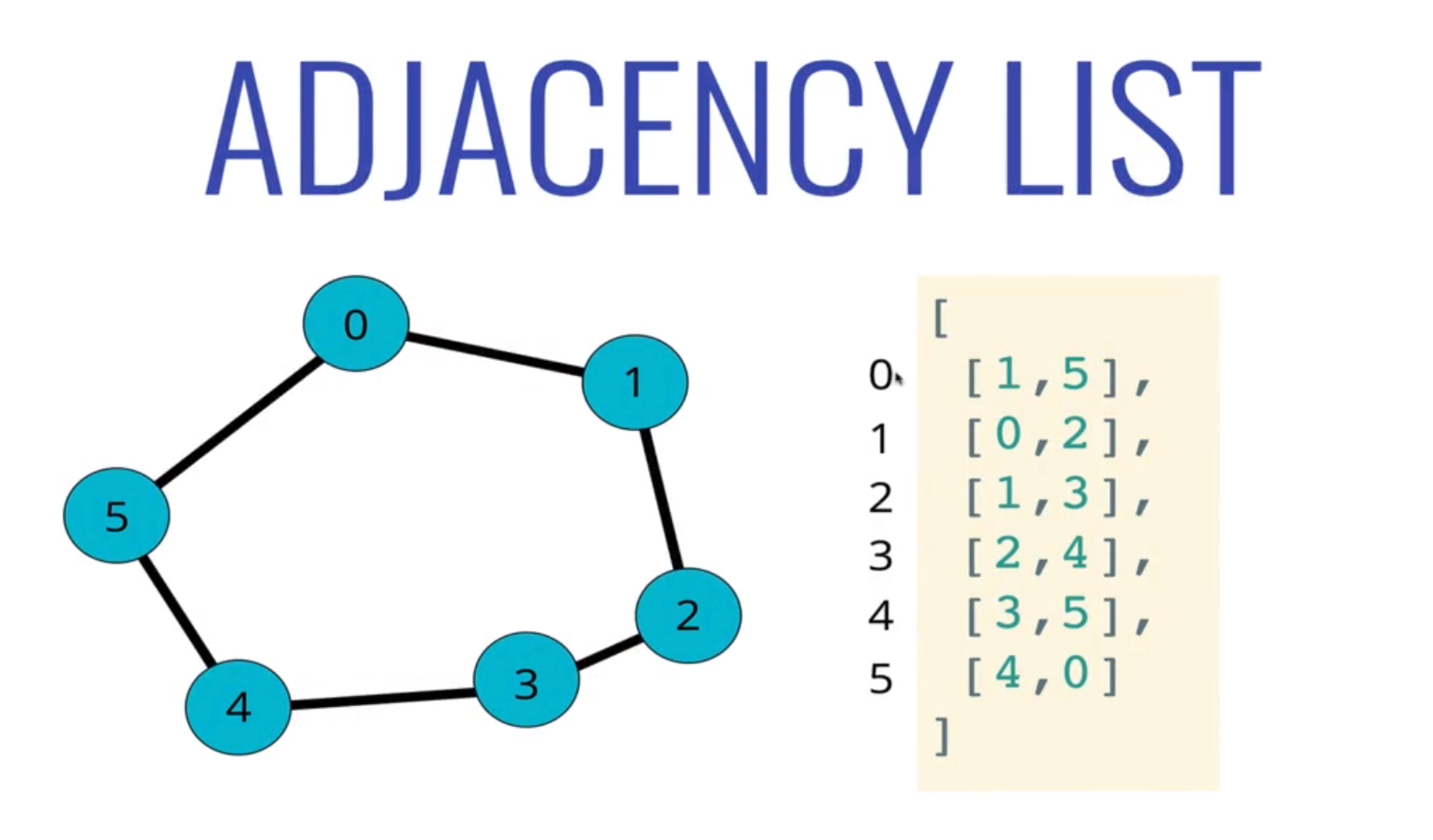
adjacency-list



如果值為 string 的話，那我們可以改用 Hash Map 來表示，例如：

  • 在 A Vertex 有連到 B 和 F，在 Adjacency List 就會是 ['B', 'F']
const adjacencyList = {};

adjacencyList['A'] = ['B', 'F']
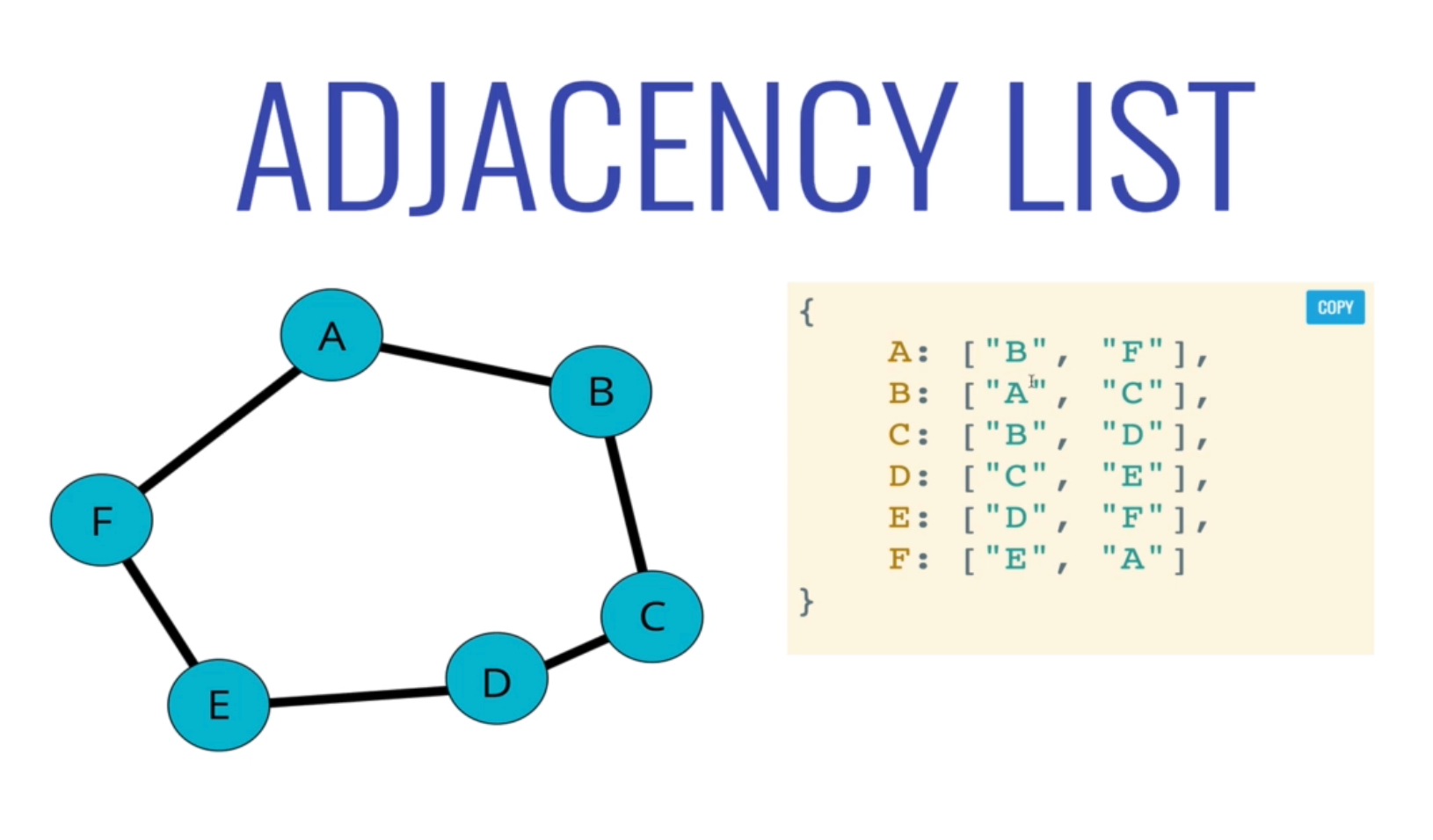
adjacency-list-hash-map


Adjacency Matrix 跟 Adjacency List 的 Big O 比較​

  • | V | - number of vertices
  • | E | - number of edges
OperationAdjacency ListAdjacency Matrix
Add Vertex✅ O(1)❌ O(|V^2|)
Add Edge✅ O(1)✅ O(1)
Remove Vertex✅ O(|E|)❌ O(|V^2|)
Remove Edge❌ O(|E|)O(1)
Query❌ O(|V| + |E|)✅ O(1)
StorageO(|V| + |E|)❌ O(|V^2|)

  • 在 Adjacency Matrix 加 Vertex，需要多增加 1 row + 1 column。在 Adjacency List 加 Vertex，只要多一對 key value

  • 但 Query 時，Adjacency Matrix 可以直接取得對應的 Vertex or Edge。Adjacency List 只能先取得 key 值，再去遍歷此 Vertex 有沒有對應的 Edge



總結來說：

Adjacency ListAdjacency Matrix
✅ 稀疏圖 (sparse graph) 中，佔更少空間❌ 稀疏圖中，佔更多空間
✅ 遍歷所有的邊 (Edges) 速度更快❌ 遍歷所有的變相對慢
❌ 查找邊 (Edges) 相對慢✅ 查找邊 (Edges) 相對快


那我們究竟要用哪一個？



Adjacency List
Adjacency List
Adjacency List
Adjacency List



因為大部分的資料都傾向呈現一個 稀疏圖 (Sparser Graph)，可以讓我們

  • 佔更少的空間
  • 遍歷所有的邊 (Edges) 速度更快


結論​

  1. Graph 是一堆 Vertex (nodes) + Edges (connections)

  2. 圖的主要元素有 Vertex 和 Edge，其中 Edge 有分為 Undirected Edge 和 Directed Edge

  3. 圖的表示法主要可以分為

    • 鄰接矩陣 (Adjacency Matrix)
    • 鄰接串列 (Adjacency List)

    且通常會用 Adjacency List 來表示 Graph，效能比較好，因為大部分的資料都傾向呈現一個 稀疏圖 (Sparser Graph)




參考資料​