Skip to main content

[Graph] 3. Graph traversal - DFS & BFS

Graph traversal 是什麼？​

通常在現實世界中，都是去針對特定情境找到對應的 vertex 去做處理，像是找到朋友朋友，主要會有以下三種行為：

  • Visiting
  • Updating
  • Checking


caution

跟 Tree 比起來，Graph traversal 沒有特定的 root / starting point



Graph Traversal 的 use cases​

以下是需要使用 Graph traversal 的 use cases：

  • Peer to peer networking (點對點網路)
  • Web crawlers（爬蟲的網站裡，還有其他的網站連結要爬）
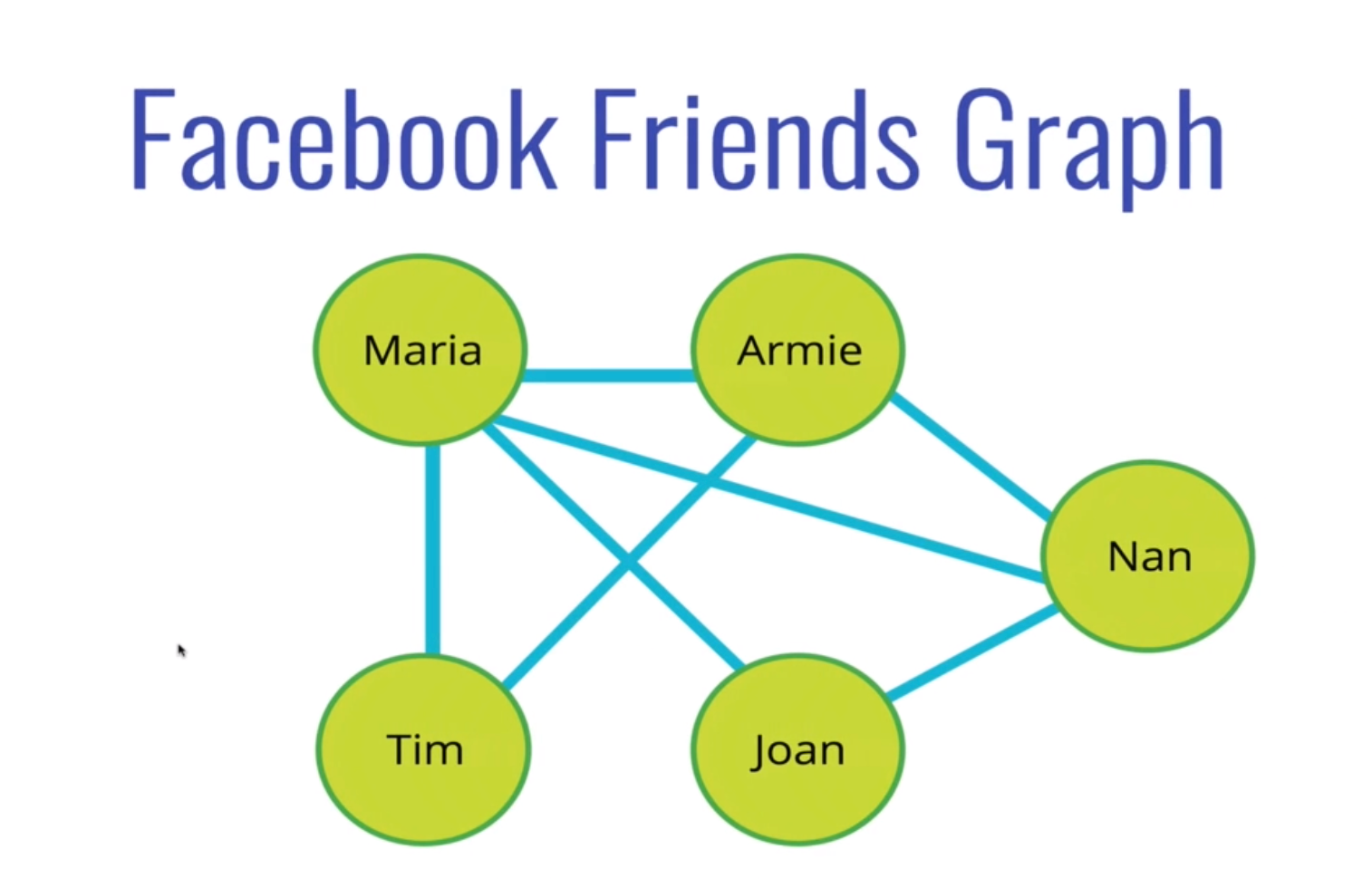
  • 推薦朋友，例如 FB friend recommendations
    (ex : Maria & Armie 都是 Nan 的朋友，Tim 也都是 Maria & Armie 的朋友 因此我們可以推薦 Tim 給 Nan)
undirected-graph-example

  • Shortest path problems (最短路徑問題)
    • GPS Navigation
    • Solving mazes
    • AI (shortest path to win the game)


Graph Traversal 的種類​

Graph traversal 跟 Tree traversal 一樣，主要會有兩種：

  • Depth-First Search (DFS)
  • Breadth-First Search (BFS)

Depth-First Search (DFS)​

從給定的 vertex 開始，沿著當下的第一個 neighbor 一路深入到最深的 vertex，然後回溯，繼續探索其他未訪問的 vertex。通常用 Recursion 達成

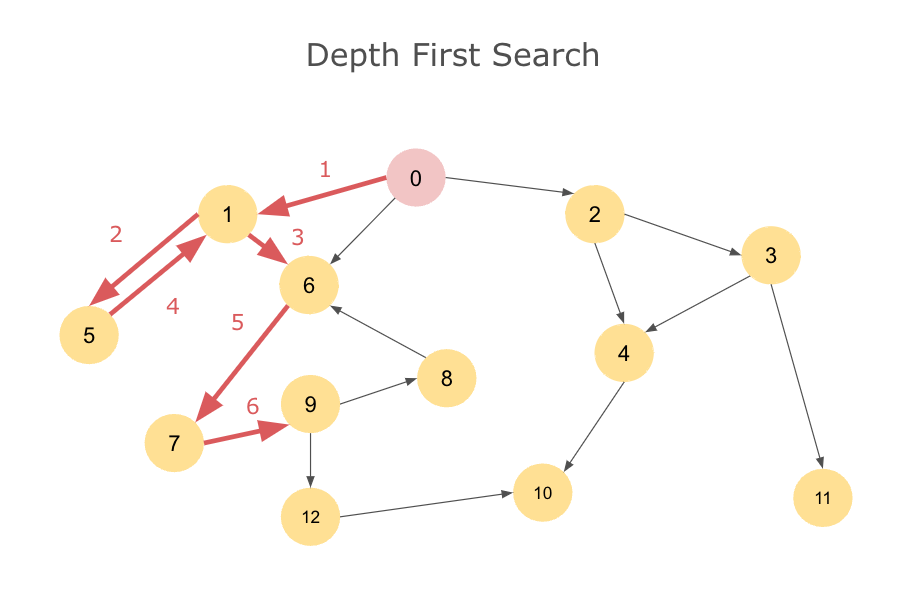
graph-depth-first-search


DFS 動畫範例​

假如從 A 點開始，然後主要依字母順序為優先方向選擇 neighbor

  1. A --> B：A 找到第一個 neighbor B，A 往 B 走
  2. B --> D：B 找到下一個 neighbor，B 往 D 走
  3. D --> E：D 找到下一個 neighbor E，D 往 E 走
  4. E --> C：E 找到下一個 neighbor C，E 往 C 走
  5. C --> E：C 走到底了，往回走到 E
  6. E --> F：E 找到第二個 neighbor F，E 往 F 走
  7. F：走到底發現所有節點都遍歷過了，停止遍歷



如果以 Adjacency List 來看的話，就會如下圖：





程式碼實現​

Pseudocode​

我們的需求如下：

  • 宣告一個 function 接收一個初始節點
  • 宣告一個陣列，儲存最終遍歷結果
  • 宣告一個物件，儲存所有經過的 vertices
  • 宣告一個 helper function，其接收一個 vertex
    • 如果 vertex 不存在，此 helper function 直接 return
    • 此 helper function 會把 vertex 加到物件裡，表示已被訪問，並且加到結果陣列裡，表示已被遍歷
    • 遍歷此 vertext adjacencyList 的所有值
    • 如果有 adjacencyList 的 vertex 還沒被訪問，持續地對那些 vertices 呼叫此 helper function
  • 以起始 vertex 呼叫此輔助函式

DFS(vertext):
    if vertex is empty
        return
    
    add vertex to results list
    mark vertex as visited

    for each neighbor in vertex's neighbors:
        if neighbor is not visited:
            DFS(neighbor)

JS 實現​

const graph = [];

const result = [];
const visited = {};


function dfs(vertex) {
    if (vertex) {
        return null;
    }

    result.push(vertex);
    visited[vertex] = true;

    for (let neighbor of graph[vertex]) {
        if (!visited[neighbor]) {
            dfs(neighbor);
        }
    }
}

dfs(root);





Breadth-First Search (BFS)​

從給定的 vertex 開始，首先訪問所有直接相鄰的節點（即第一層），然後依次訪問這些節點的鄰居（即第二層），以此類推。這種方法使用 Queue來記錄訪問的節點。

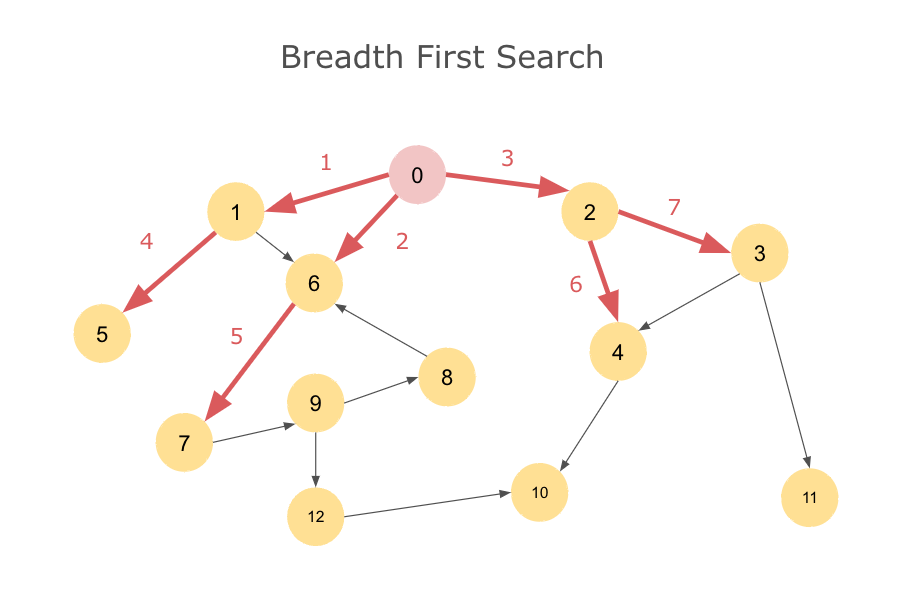
graph-breadth-first-search



BFS 動畫範例​

假如從 A 點開始，然後主要依字母順序為優先方向選擇 neighbor

  1. A --> B：A 找到第一個 neighbor B，A 往 B 走
  2. A --> E：A 找到下一個 neighbor E，A 往 E 走
  3. B --> C：B 找到下一個 neighbor C，B 往 C 走
  4. B --> D：B 找到下一個 neighbor D，B 往 D 走
  5. E --> F：E 找到下一個 neighbor F，E 往 F 走
  6. F：走到底發現所有節點都遍歷過了，停止遍歷




如果以 Adjacency List 來看的話，就會如下圖：





程式碼實現​

Pseudocode​

  • 此函式接收一個起始 vertex
  • 宣告一個 queue，並將起始 vertex 放進去
  • 宣告一個 array，儲存所有訪問過的節點
  • 宣告一個 object，儲存所有訪問過的節點
  • 將起始 vertex 標註為 visited
  • 只要 queue 內還有 vertex，就對 queue 做遍歷
    • 移除 queue 的 1st vertex，並將 vertex push 到 visited array
    • 遍歷此 vertex 對應的 adjacencyList 的所有元素
    • 如果遍歷到的 vertex 不在 visited object 裡，將其標示為 visited 且 enqueue 此 vertex
  • 一旦完成遍歷，回傳訪問過的 nodes

JS 實現​

const graph = [];

const result = [];

function bfs(vertex) {
    const queue = [vertex];
    const result = [];
    const visited = {};

    visited[vertex] = true;

    while (queue.length > 0) {
        const vertex = queue.shift();
        result.push(vertex);

        const adjacencyList = graph[vertex];

        for (let neighbor of adjacencyList) {
            if (!visited[neighbor]) {
                visited[neighbor] = true;
                queue.push(neighbor);
            }
        }
    }

    return result;
}

bfs(root);



結論​

  1. Graph traversal 分為兩種：DFS & BFS
  2. DFS 沿著 neighbor 一直深入到最深的 vertex，然後回溯，直到遍歷所有 vertex
  3. BFS 一層一層的遍歷所有 neighbors，直到遍歷所有 vertex



參考資料​