[LeetCode] 什麼是 Heap?
什麼是 Heap?
Heap 是一種特殊的 Tree,它滿足以下性質:
- 它是一個完全二叉樹(Complete Binary Tree)
- parent node 的值總是會一直大於 child node (Max Heap) 或小於 child node (Min Heap)
範例如下
最大堆(Max Heap)
- parent nodes 總是比 child nodes 大
- parent node 最多只能有 2 個 childe nodes
- Binary Heap 能越緊密就越緊密 (compact),每個 node 的 children 會盡可能被填滿,且會從左邊開始填,不像 Binary search tree 可以 node 都在同一邊,像 Linked List 一樣
最小堆(Min Heap)
- parent nodes 總是比 child nodes 小
- parent node 最多只能有 2 個 childe nodes
❌ Not a Binary Heap
- 33 < 41
- 41 > 39
沒有所有節點符合都大於 or 都小於的規律
我們為什麼需要知道 Heap?
Binary Heap 對後續建立一些顯算法或資料結構非常重要,像是:
- Binary Heap 本身:以 log n 的時間複雜度,來找到最大或最小的值
- Priority Queues:針對自定義的排序規則,來取出前 K 個 (或第 K 個) 最大或最小的優先的值
- Graph traversal:像是:
- Dijkstra's Algorithm (單元最短路徑)
- Prim's Algorithm (最小生成樹)
如何實作 Heap?
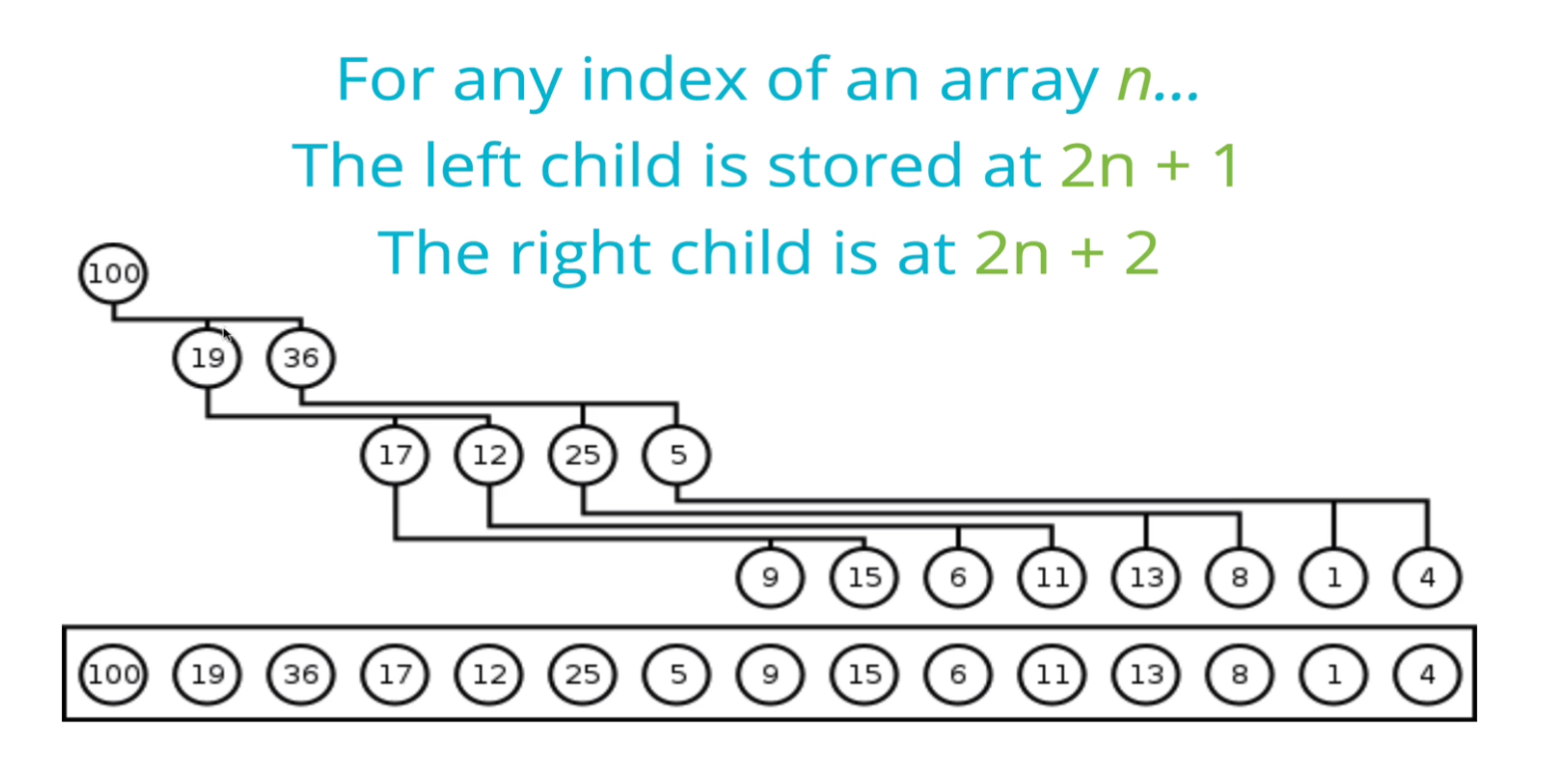
因為 Heap 是 Complete Binary Tree,我們可以用層序遍歷 (Level Order Traversal) 的方式,將其表示為一個陣列,像是:
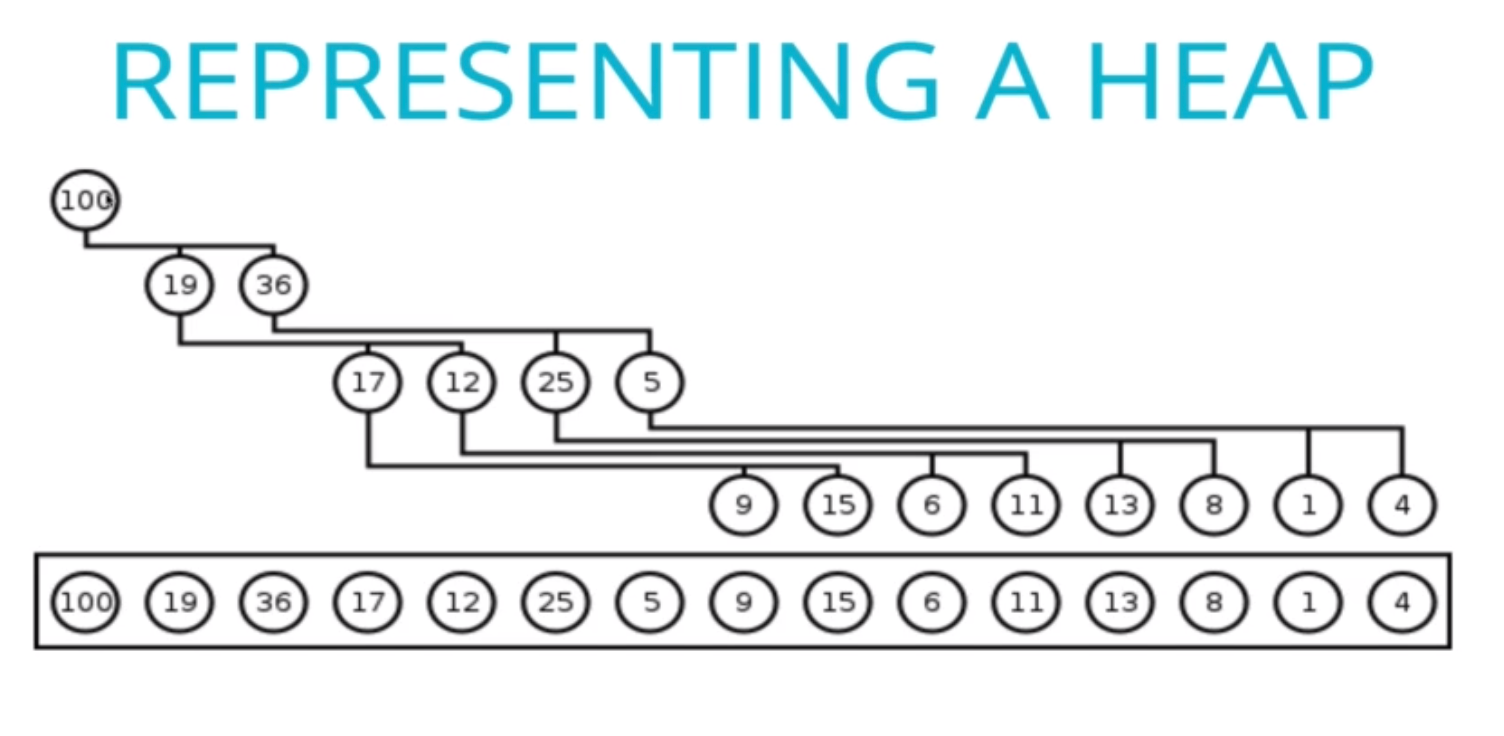
如何尋找 children nodes
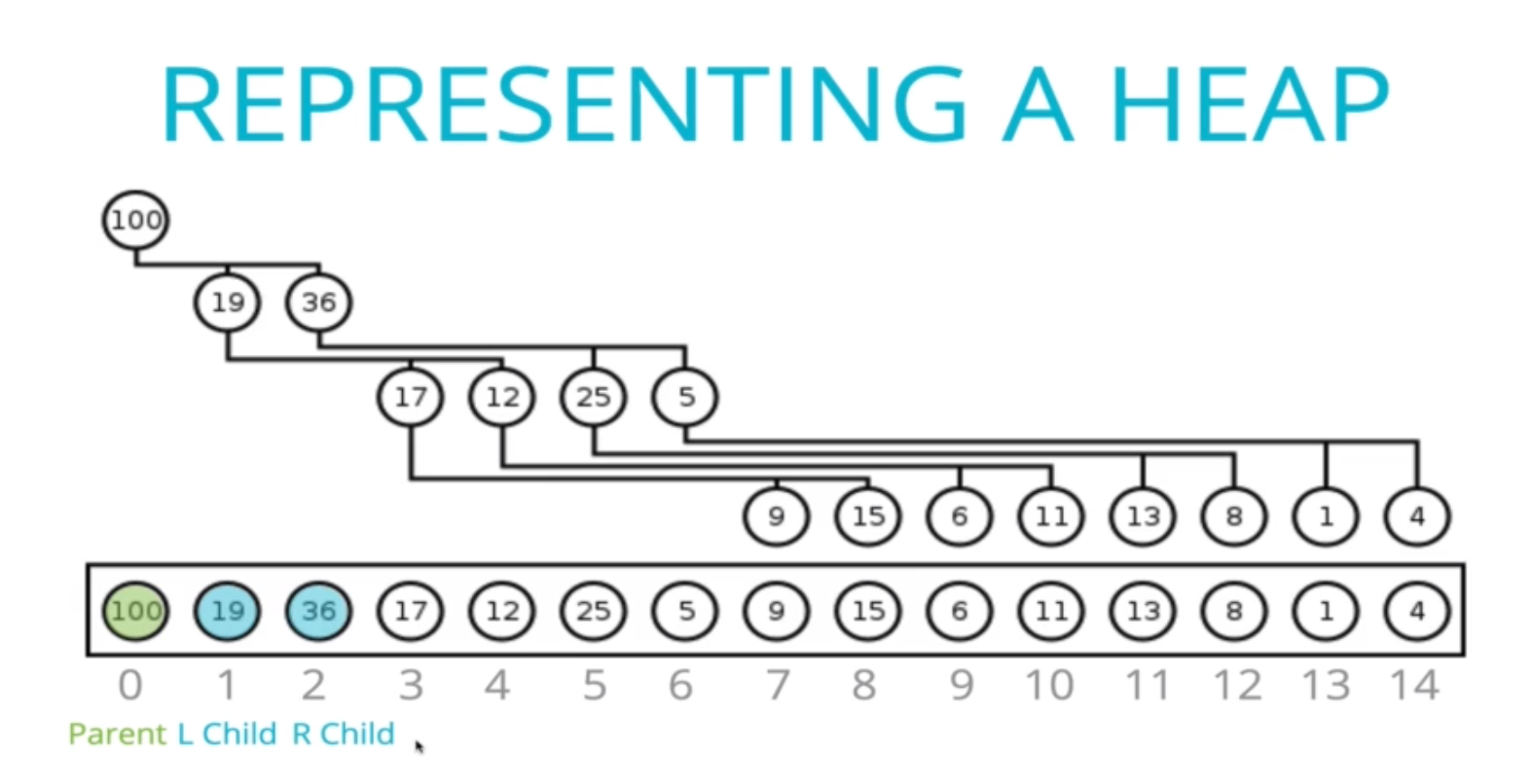
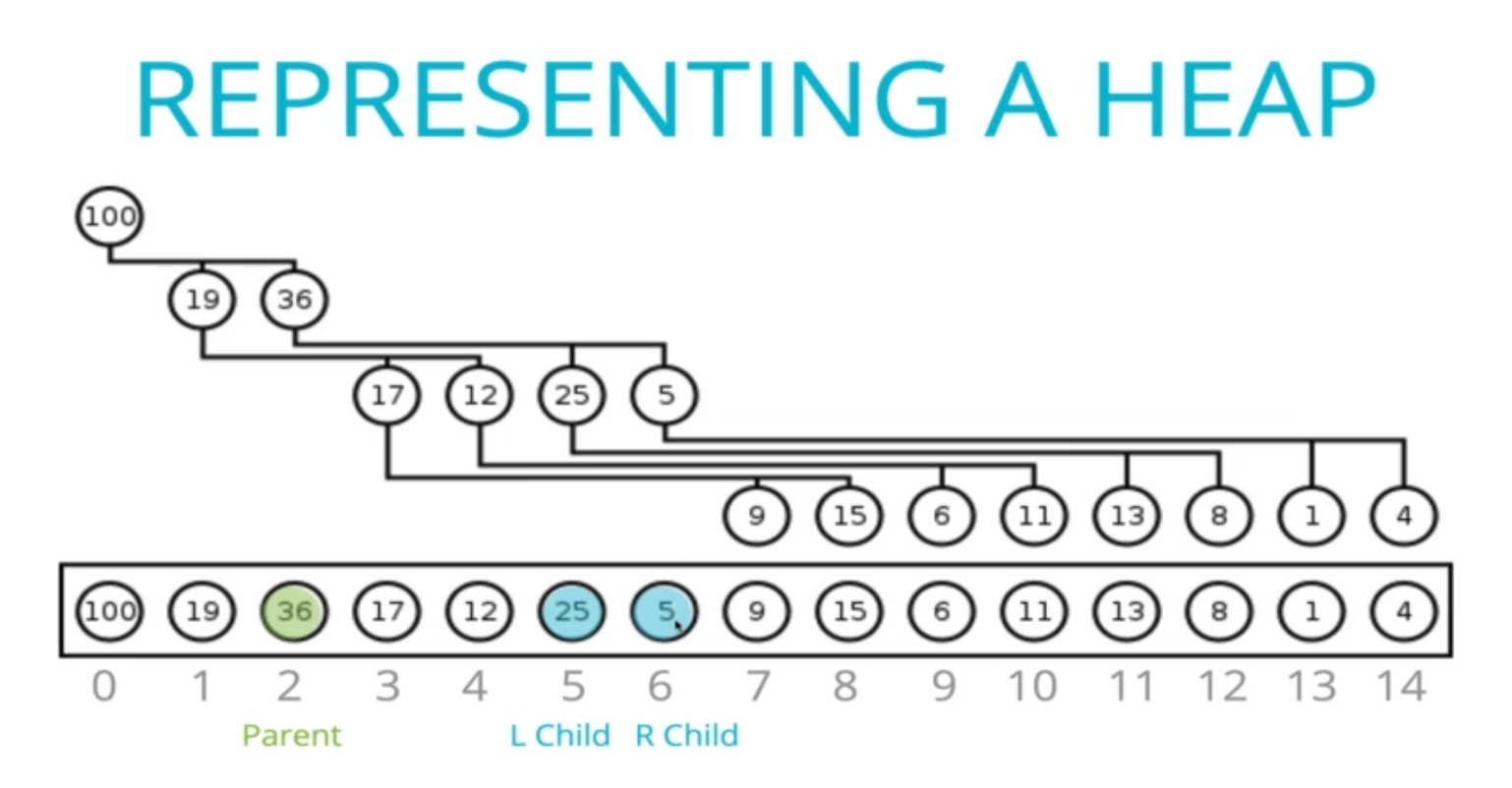
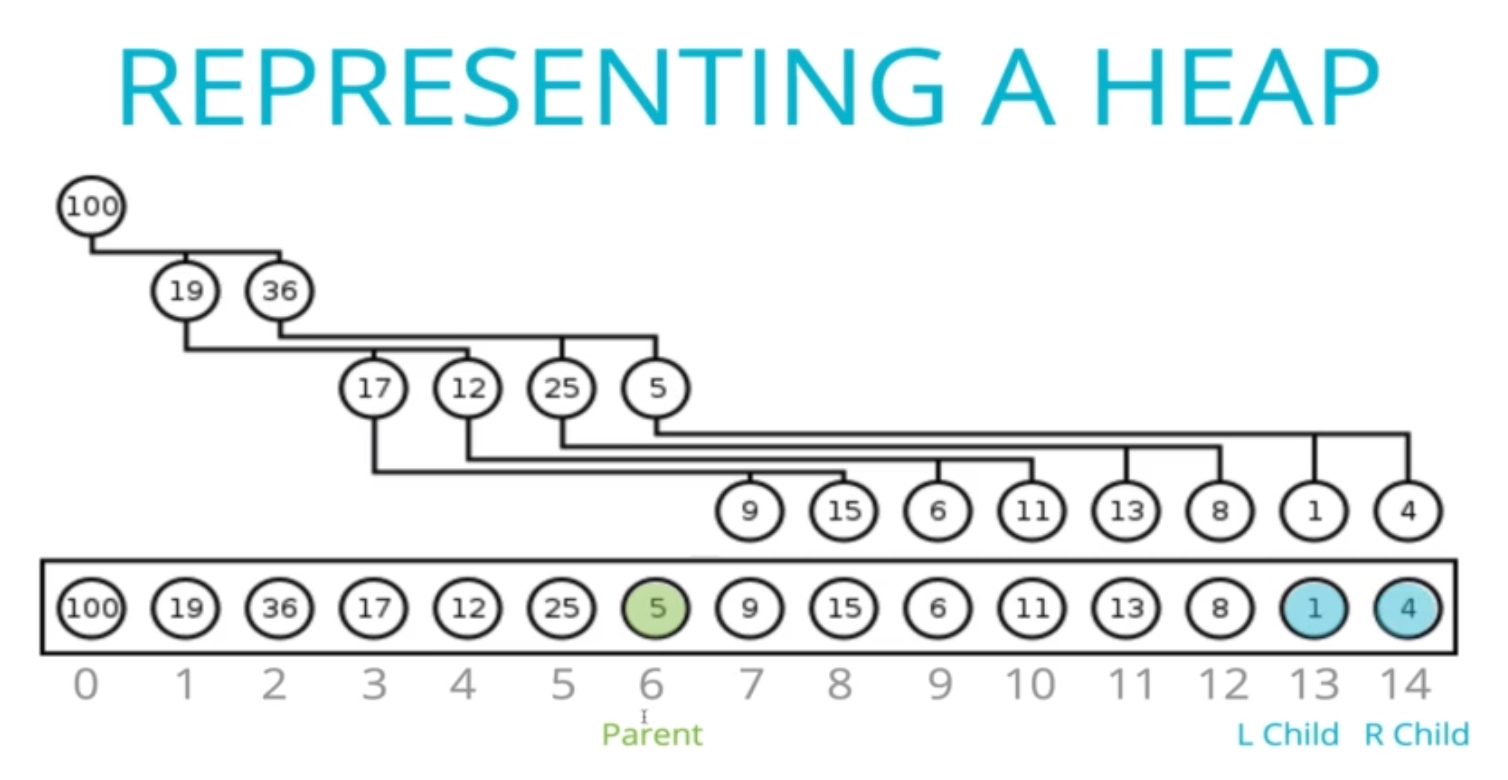
在上圖,我們可以發現,parent node 跟 children node 是有特殊關係的,我們可以依下面三張圖來觀察:
- 當 parent node 的 index 是 0,left child 為 1, right child 為 2
- 當 parent node 的 index 是 2,left child 為 5, right child 為 6
- 當 parent node 的 index 是 6,left child 為 13, right child 為 14
根據上述的觀察和數學上的一些歸納,我們可以得到一個結論:
若 1 個 node 的位置在 n
- Left child 存在於:2n + 1
- Right child 存在於:2n + 2
如何尋找 parent node
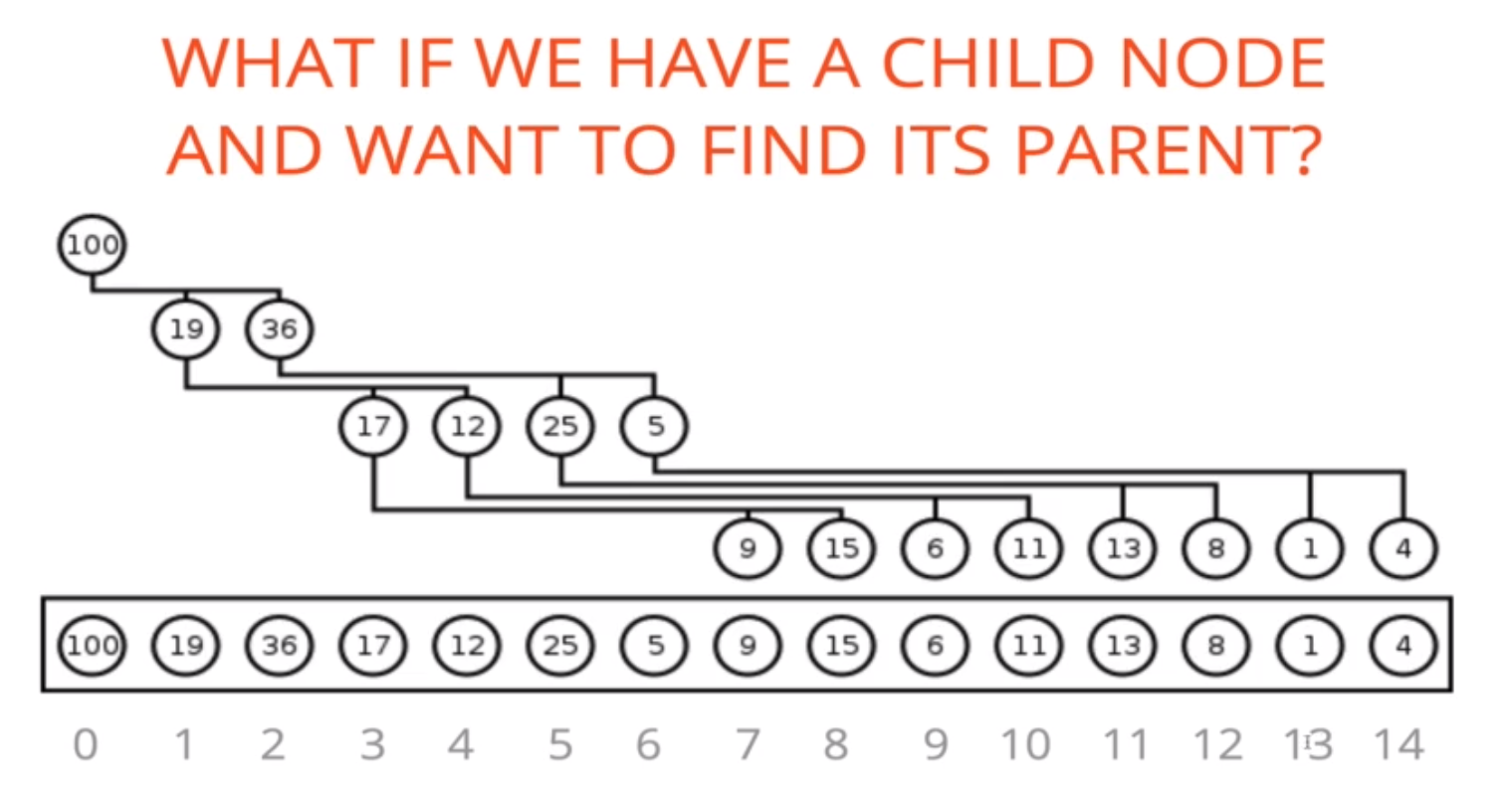
反之,我們可以從 find children nodes 的公式,反推 parent node 的公式:
若 1 個 node 的位置在 n
- Parent node 存在於:Math.floor((n - 1) / 2)
結論
- Heap 是一種特殊的 Complete Binary tree
- Heap 可以幫助後續的資料結構 & 演算法,像是:
- Heap, Priority Queue 用來做 kth 最大/最小值的運算
- Graph 的 Traversal 演算法,像是 Dijkstra's Algorithm, Prim's Algorithm
- Heap 可以用 array 來表示,並藉由特殊關係取得 parent node 或 children node 的 index