[Graph] 4. Disjoint Set (Union & Find)
什麼是 Disjoint Set? 為什麼需要 Disjoint Set?
我們在處理 Graph 問題時,會需要知道 2 個點是否相連,而我們需要一種有效率的資料結構與演算法來處理這個問題
如以下的範例,我們可以多快地找出以下 2 點之間:
- 0 跟 3 是否相連?
- 1 跟 5 是否相連?
- 7 跟 8 是否相連?
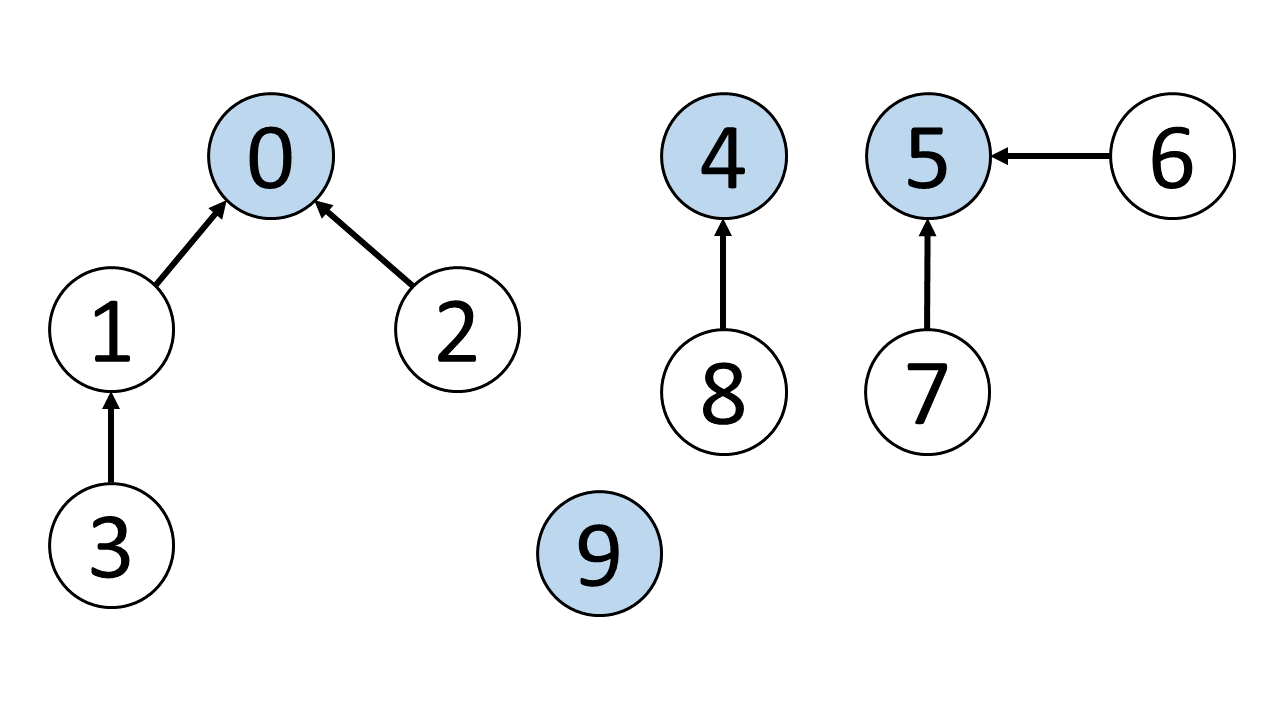
我們可以利用 Disjoint Set (Union & Find) 這個資料結構來處理這類型問題
通常我們在做這類型的題目,會聽到 Disjoint Set 跟 Union Find 這兩個名詞,這兩個名詞其實是同一個東西, 但差別在於:
- Disjoint Set:主要在描述資料結構,表示各群不相交的 vertices 集合
- Union Find:主要在描述演算法,分別為 Union 與 Find,Union 用於將兩個點連結,Find 用於找查 vertice 的 root node
相關術語
- Parent node: vertex 直接對應的 parent node
- Root node:沒有 parent 的 node,或者說自己就是自己的 parent node
(a node without a parent node; it can be viewed as the parent node of itself.)
Disjoint Set 的運作流程
假設我們現在有 0 ~ 9 的 vertices,並且在這個 Graph 的 edges 如下:
[
[0, 1], [0, 2], [1, 3],
[4, 8], [5, 6], [5, 7]
]
下面我們就用一個 Slides 的圖示來介紹 Disjoint Set 的運作流程
我們透過 edge 連結各點,來將相關連的 vertices 各自歸類到不同的 set, 最後在 Slides 8,我們就可以用最終的 sets 來判斷 2 點是否相連,例如:
0, 3:有相同的 root,所以相連1, 5:沒有相同的 root,所以不相連7, 8:沒有相同的 root,所以不相連
資料結構的運作
如果我們把 Disjoint Set 的運作轉成程式的資料解構,我們可以用 1 Array 來表示,其中:
- 每個 index 代表每個 vertex
- 每個 index 的 value 代表每個 vertex 的 parent node
並且,如果我們想知道 2 vertices 是否相連,我們可以透過 2 個 vertices 的 root node 是否相同來判斷, 我們可以利用 parent array 來找到每個 vertex 的 root node,並利用 root node 的 parent 就是自己本身的特性: 以上圖的例子來說:
- ✅ (0,3) 是相連的,因為
findRoot(0) === 0:parentArray[0] = 0 --> 0findRoot(3) === 0:parentArray[3] = 1 --> parentArray[1] = 0 --> parentArray[0] = 0 --> 0
- ❌ (1,5) 是不相連的,因為
findRoot(1) === 0:parentArray[1] = 0 --> parentArray[0] = 0 --> 0findRoot(5) === 5:parentArray[5] = 5
- ❌ (7,8) 是不相連的,因為
findRoot(7) === 5:parentArray[7] = 5 --> parentArray[5] = 5 --> 5findRoot(8) === 4:parentArray[8] = 4 --> parentArray[4] = 4 --> 4
重要 functions
在 Disjoint Set 中,我們有 2 個重要的 functions,可以幫我們解決多數的問題:
find:找到給定 vertex 的 root nodeunion:將輸入的 2 個 input vertices 連結起來,並設為同一個 root node
兩種實作模式
根據不同的需求,我們可以用不同的實作模式,分別達到最好的 find 或 union 的效率:
- Implementation with Quick Find:
find:O(1)union:O(N)
- Implementation with Quick Union:
find:O(N)union:O(N)
Quick Find
如果我們要快速找到指定 vertex 的 root node,我們可以將 array value 改為儲存 Root vertex, 這樣一來,我們就可以在 O(1) 的時間內找到指定 vertex 的 root node
但代價是:我們在 union 的時候就需要 O(N) 的時間來更新所有相關的 vertices
以下列的例子來說,我們有兩組 sets,分別以 0, 2 為 root node,當我們連結 0, 2 時,我們也要同時更改 root node 為 2 的所有 vertices, 將其 root node 改為 2
JavaScript 實作
我們主要需要實作三個 methods:
find:找到指定 vertex 的 root nodeunion:將輸入的 2 個 input vertices 連結起來,並設為同一個 root nodeconnected:確認兩點是否相連
class UnionFind {
root = [];
// 一開始先預設每個 vertex 的 root node 為自己
constructor(size) {
for (let i = 0; i < size; i++) {
this.root[i] = i;
}
}
// 直接回傳 root array 的值
find(x) {
return this.root[x];
}
// 1. 先找到 x, y 的 root node
// 2. 將 y 的 root node 設為 x 的 root node
// 3. 將 root node 為 y 的其他 vertices 的 root node 也一起更新成 x 的 root node
union(x, y) {
const rootX = this.find(x);
const rootY = this.find(y);
if (rootX !== rootY) {
this.root[y] = rootX;
for (let i = 0; i < this.root.length; i++) {
if (this.root[i] === rootY) {
this.root[i] = rootX;
}
}
}
}
// 確認兩點是否相連,透過 2 vertices 的 root node 來判斷
connected(x, y) {
return this.find(x) === this.find(y);
}
}
Complexity
對於 Quick Find,find 可以達到 O(1) 的效率,但 union 需要檢查所有 vertices 的 root node 是否需要更改,需要 O(N) 的時間
| Union-find Constructor | Find | Union | Connected | |
|---|---|---|---|---|
| Time Complexity | O(N) | O(1) | O(N) | O(1) |
| Space Complexity | O(N) | |||
Quick Union
如果我們要快速連結 2 vertices,我們保持 parent array 的值為 parent node,會是最有效的方式
如下圖中,當我們連結 0, 4 時,我們只需要將 4 的 parent node 設為 0,而不需要更新其他 vertices 的 parent node,在 union 中減少非常多的操作
JavaScript 實作
我們需要實作三個 methods 跟 Quick Find 相同,主要是 highlight 的部分實作上有差別:
find:找到指定 vertex 的 root nodeunion:將輸入的 2 個 input vertices 連結起來,並設為同一個 root nodeconnected:確認兩點是否相連
class UnionFind {
root = [];
constructor(size) {
for (let i = 0; i < size; i++) {
this.root[i] = i;
}
}
// 一直去找尋 parent node,直到 parent node 就是自己本身
find(x) {
while (this.root[x] !== x) {
x = this.root[x];
}
return x;
}
// 1. 先找到 x, y 的 root node
// 2. 將 y 的 root node 設為 x 的 root node
union(x, y) {
const rootX = this.find(x);
const rootY = this.find(y);
if (rootX !== rootY) {
this.root[y] = rootX;
}
}
// 確認兩點是否相連,透過 2 vertices 的 root node 來判斷
connected(x, y) {
return this.find(x) === this.find(y);
}
}
Complexity
對於 Quick Union,find 需要一直去找尋 parent node,直到 parent node 就是自己本身,需要 O(N) 的時間,但這是 worst case 的狀況,如下圖,
而 union 因為用到了 find method,所以時間複雜度也是 O(N)
| Union-find Constructor | Find | Union | Connected | |
|---|---|---|---|---|
| Time Complexity | O(N) | O(N) | O(N) | O(N) |
| Space Complexity | O(N) | |||
Quick Union vs Quick Find
若要從 0 組到 n 的 union:
| Find | Union | |
|---|---|---|
| Quick Find | O(1) | N * O(N) === O(N^2) |
| Quick Union | O(N) (In worst case) | N * O(N) === O(N^2) (In worst case) |
平均下來
Quick Union 的效率會比 Quick Find 來得好
Quick Union Optimizations
由於 Quick Union 在不管在 find 或 union 的 worst case 的狀況下,會需要 O(N) 的時間,我們希望可以再進一步優化:
我們有以下兩種優化方法:
- Union by Rank:針對
union的時間複雜度做優化 - Path Compression:針對
find的時間複雜度做優化
我們就來一一介紹
Union by Rank
如果我們在 union 時沒有特別處理,在最壞的情況下,我們的 tree 會變成一個 linked list,這樣一來,find 的時間複雜度就會變成 O(N)
但我們可以利用一些技巧,在 union 做一些判斷,讓連接後的 graph 的廣度及深度更平衡,
這樣在進行 find 時,效率會更好,進而間接優化 union 的時間複雜度
方法很簡單,如下:
- 我們先得出出兩個 set 的深度
- 以深度較深的 set 的 root node 為基準,將深度較淺的 set 連接到深度較深的 set 上
這樣我們就可以避免最壞的 O(N) 的狀況
JavaScript 實作
- 宣告一個 rank array,用來儲存每個 vertex 的深度
- 先預設每個 vertex 的深度為 1
- 在
union時,比較兩個 set 的深度,- 將深度較淺的 set 連接到深度較深的 set 上
- 如果深度相同,則將其中一個 set 連接到另一個 set 上,並將被接上的 vertex rank 加 1
class UnionFind {
root = [];
rank = [];
constructor(size) {
for (let i = 0; i < size; i++) {
root[i] = i;
rank[i] = 1;
}
}
union(x, y) {
const rootX = this.find(x);
const rootY = this.find(y);
if (rootX !== rootY) {
// 看哪邊較大,就設哪邊為 root node
// 如果兩邊一樣大,那我們就隨邊設一邊為 root node,並且將 rank +1,表示會再多 1 的高度
if (rank[rootX] > rank[rootY]) {
root[rootY] = rootX;
} else if (rank[rootX] < rank[rootY]) {
root[rootX] = rootY;
} else {
root[rootY] = rootX;
rank[rootX] += 1;
}
}
}
}
Complexity
- Time Complexity
- 對於
union-find,我們需要建立 2 個 size N 的 array - 對於
find,在最糟的情況下,我們重複連結深度相同的 graph,graph height 最多是 log (N) + 1,所以find的時間複雜度是 O(log N) - 對於
union和connected,我們需要先find2 個 vertices 的 root node,所以時間複雜度是 O(log N)
- 對於
- Space Complexity
- 對於
union-find,我們需要建立 2 個 size N 的 array
- 對於
| Union-find Constructor | Find | Union | Connected | |
|---|---|---|---|---|
| Time Complexity | O(N) | O(log N) | O(log N) | O(log N) |
| Space Complexity | O(N) | |||
Path Compression
除了在 union 優化,我們也可以針對 find method 做優化,我們可以讓 find 的時間複雜度機乎變成跟 Quick Find 一樣,逼近於 O(1)
我們在第一次執行 find 時,我們可以利用 Recursion 的技巧,來取得 root node,並將每個 vertex 的 parent node 設為 root node,
這樣一來,在第二次以後執行 find 時,時間複雜度就會變成 O(1)
JavaScript 實作
- 先取得 x 的 parent node
- 再利用 Recursion 的技巧,再往下找 parent 的 parent,直到找到 root node
- 並將 x 的 parent node 設為 root node
class UnionFind {
...
find(x) {
if (this.root[x] === x) {
return x;
}
const parent = this.root[x];
const rootX = this.find(parent);
this.root[x] = rootX;
return rootX;
}
...
}
Complexity
- Time Complexity
- 對於
find,在最好的情況下,也就是只有一層的平衡術,時間複雜度為 O(1),在最壞的情況下,也就是編成一個 linked list,時間複雜度為 O(N), 這樣平均下來,時間複雜度為 O(log N) (詳細可以參考 Top-Down Analysis of Path Compression)
- 對於
| Union-find Constructor | Find | Union | Connected | |
|---|---|---|---|---|
| Time Complexity | O(N) | O(log N) | O(log N) | O(log N) |
| Space Complexity | O(N) | |||
優化完的 Quick Union
JavaScript 實作
class UnionFind {
root = [];
rank = [];
constructor(n) {
for (let i = 0; i < n; i++) {
this.root[i] = i;
this.rank[i] = 1;
}
}
find(x) {
if (this.root[x] === x) {
return x;
}
const parent = this.root[x];
const rootX = this.find(parent);
this.root[x] = rootX;
return rootX;
}
union(x, y) {
const rootX = this.find(x);
const rootY = this.find(y);
if (rootX !== rootY) {
if (this.rank[rootX] > this.rank[rootY]) {
this.root[rootY] = rootX;
} else if (this.rank[rootX] < this.rank[rootY]) {
this.root[rootX] = rootY;
} else {
this.root[rootY] = rootX;
this.rank[rootX] += 1;
}
}
}
connected(x, y) {
return this.find(x) === this.find(y);
}
}
Complexity
再經過 Union by Rank 和 Path Compression 的優化後,find 的時間複雜度變成 O(α(N)),
其中 α(N) 是 Ackermann function 的反函數,增長速度會非常慢,其值會非常接近於 O(1),
union 和 connected 的時間複雜度也會因為 find 的時間複雜度變成 O(α(N))
| Union-find Constructor | Find | Union | Connected | |
|---|---|---|---|---|
| Time Complexity | O(N) | O(α(N)) | O(α(N)) | O(α(N)) |
| Space Complexity | O(N) | |||
結論
- Disjoint Set 是用來判斷兩點是否相連
- 有兩種方法可以實作 Disjoint Set:Quick Find 和 Quick Union,Quick Union 的效率比較好
- Quick Union 可以再進一步優化,利用 Union by Rank 優化
union的時間複雜度,並利用 Path Compression 優化find的時間複雜度 - Quick Union 經過優化後,
find的時間複雜度變成 O(α(N)),幾乎逼近於 O(1),union和connected的時間複雜度也會連帶變成 O(α(N))